How to Do Ternary or Trinary, Base 3 Numbering System Conversions Lesson / Tutorial Examples

Latest update: November 24, 2024

If you understand the everyday decimal (base 10) number system, then you already understand the ternary, base 3 counting and numbering system. You just don’t know you know yet. The complete lesson immediately follows the short semantics note about "ternary" versus "trinary".

Base 3 Conversion - Base 3 to Base 10 and Back - 0 1 2

How to Learn the Ternary Base 3 Numbering System

A complete lesson and examples.

Semantics Note

Ternary is the primary descriptor used to identify base 3 (using the digits 0 1 2) in mathematics as relates to numbering systems. Trinary is the primary descriptor used to identify base three as relates to logic (using the digits -1 0 +1); but the term has also been used in place of ternary. This page does not address the logic definition of trinary. This page is about and explains the base 3 number system; usually called ternary, but sometimes referred to as trinary.

A Quick Review of Base 10 Structure...

Base 10 Decimal Orders of Magnitude

1 · 10 · 100 · 1,000 · 10,000 · 100,000

Positional

100,000 · 10,000 · 1,000 · 100 · 10 · 1

We use the base 10 numbering/counting system in our day-to-day living. Base 10 has ten numbers (0-9) and orders of magnitude that are times ten.

• The lowest order number represents itself times one.
• The next order number represents itself times 10.
• The next order number represents itself times 10 x 10, or itself times 100.
• The next order of magnitude would be 10 x 10 x 10, or 1000.

And so on. A base 10 example would be the number 3528. This number means that there are:

• Eight 1’s,
• two 10’s,
• five 100’s,
• and three 1000's.

Which represents 8 + 20 + 500 + 3000 for a total of 3528.

The Ternary or Base 3 Numbering System...

...uses the same structure, the only difference being the orders of magnitude. Base 3 or ternary has three numbers: 0, 1, and 2.

The orders of magnitude are times three.

• The lowest order number represents itself times one.
• The next order number represents itself times 3.
• The next order number represents itself times 3 x 3, or itself times 9.
• The next order of magnitude would be 3 x 3 x 3, or itself times 27.
• The next order of magnitude would be 3 x 3 x 3 x 3, or itself times 81.

And so on.

Orders of Magnitude in Base 3

• 1 · 3 · 9 · 27 · 81 · 243 · 729 · 2,187 · 6,561

Positional

• 6,561 · 2,187 · 729 · 243 · 81 · 27 · 9 · 3 · 1

A basic, first example of a ternary number would be the base 3 number 11111. This would mean there are:

• one 1,
• one 3,
• one 9,
• one 27,
• and one 81.

Which represents 1 + 3 + 9 + 27 + 81 for a total of 121 in Base 10 decimal.

Another base 3 example would be the number 1120. This number means that there are:

• No 1’s,
• two 3’s,
• one 9,
• and one 27.

Which represents 0 + 6 + 9 + 27 for a total of 42 in base 10 decimal.

Another base 3 example would be the number 2101. This number means there are:

• One 1,
• No 3's,
• One 9,
• And two 27’s.

Which represents 1 + 0 + 9 + 54 for a total of 64 in base 10 decimal.

More Ternary (Base 3) to Base 10 Conversion Examples

9 · 3 · 1	9 · 3 · 1	27 · 9 · 3 · 1
0=0	110=12	220=24
1=1	111=13	221=25
2=2	112=14	222=26
10=3	120=15	1000=27
11=4	121=16	1001=28
12=5	122=17	1002=29
20=6	200=18	1010=30
21=7	201=19	1011=31
22=8	202=20	1012=32
100=9	210=21	1020=33
101=10	211=22	1021=34
102=11	212=23	1022=35

(Convenience relist)

Orders of Magnitude in Base 3

• 1 · 3 · 9 · 27 · 81 · 243 · 729 · 2,187 · 6,561

Positional

• 6,561 · 2,187 · 729 · 243 · 81 · 27 · 9 · 3 · 1

Other base numbering systems:  Try https://mathschool.etsy.com.

- End of Article -

Re: Using Mobile?
Home: site intro and featured articles/resources.
View Web Version: displays Main Menu article categories (will be located below), 

additional site info (below and side), search function, translation function.

I first published this article at another website on 09/19/10. However, to keep the information current, relocating to websitewithnoname.com was best. This copyrighted article has served people well for years.

How to Do Duodecimal, Dozenal, Base 12 Number System Conversions — Examples, Math Problems

Latest update: November 24, 2024

If you understand the everyday decimal (base 10) number system, then you already understand the duodecimal, base 12, dozenal counting and numbering system. You just don’t know you know yet. The complete lesson immediately follows the short introduction.

For other base numbering systems, check out mathschool.etsy.com.

Timekeeping is heavily reliant on the number 12 and its composites (evenly divisible numbers: 2, 3, 4, 6).

How to Learn the Duodecimal, Dozenal, Base 12 Numbering System

An Interesting "Political" Side Note.

The base 12 numerical system, also known as the duodecimal or dozenal system, is just like all the other base numbering and counting systems. However, this is the only base numbering system which has a "political" aspect to it. This has to do with the number 12 being a very useful number and as to which symbols to use for the base 10 numbers "10" and "11".

If one wishes to remain within the standardized structure of hexadecimal and the other base numbering and counting systems up to and including base 36, then the use of sequential numbers and letters should be used. Thus, as in hexadecimal, the base 10 number "10" is equal to the base 12 number "A", and the base 10 number "11" is equal to the base 12 number "B".

Others advocate the use of different symbols, some examples being:

• 10 = T
• 10 = X
• 11 = E

This how-to tutorial will stick with the base 2 through base 36 mathematical "standard" of 10 being designated by "A" and 11 being designated by "B".

Complete Lesson and Examples

A quick review of the decimal, base 10 structure...

Base 10, Decimal Orders of Magnitude
1 · 10 · 100 · 1,000 · 10,000 · 100,000
Positional
100,000 · 10,000 · 1,000 · 100 · 10 · 1

We use the base 10 numbering/counting system in our day-to-day living. Base 10 has ten numbers (0-9) and orders of magnitude that are times ten.

• The lowest order number represents itself times one.
• The next order number represents itself times 10.
• The next order number represents itself times 10 x 10, or itself times 100.
• The next order of magnitude would be 10 x 10 x 10, or 1000.

And so on.

A base 10, decimal example would be the number 7824. This number means there are:

• Four 1’s,
• Two 10’s,
• Eight 100’s,
• And seven 1000's.

Which represents 4 + 20 + 800 + 7000 for a total of 7824.

The duodecimal, base 12, dozenal numbering system...

...uses the same structure, the only difference being the orders of magnitude. Base 12 aka duodecimal has twelve numbers (0 thru B). The numbers are:

• 0 = 0, 1 = 1, 2 = 2, 3 = 3, 4 = 4, 5 = 5, 6 = 6, 7 = 7, 8 = 8, 9 = 9
• A = 10
• B = 11

The orders of magnitude are times twelve.

• The lowest order number represents itself times one.
• The next order number represents itself times 12. The next order number represents itself times 12 x 12, or itself times 144.
• The next order number represents itself times 12 x 12 x 12, or itself times 1728.
• The next order number represents itself times 12 x 12 x 12 x 12, or itself times 20736.

And so on.

Duodecimal, Base 12 Orders of Magnitude

1 · 12 · 144 · 1728 · 20736 · 248832

Positional

248832 · 20736 · 1728 · 144 · 12 · 1

A basic, first example of a duodecimal number would be the base 12 number 11111. This would mean there is:

• one 1,
• one 12,
• one 144,
• one 1728,
• and one 20736.

Which represents 1 + 12 + 144 + 1728 + 20736 for a total of 22621 in base 10 decimal.

Another base 12 example would be the number 2B9A. This number means there are:

• Ten 1’s,
• Nine 12’s,
• Eleven 144’s,
• And two 1728’s.

Which represents 10+108+1584+3456 for a total of 5158 in base 10 decimal.

Another base 12 example would be the number A51B. This number means there are:

• Eleven 1’s,
• One 12,
• Five 144’s,
• And ten 1728’s.

Which represents 11+12+720+17280 for a total of 18023 in base 10 decimal.

Convenience relist...

Base 12, Duodecimal Orders of Magnitude
1 · 12 · 144 · 1728 · 20736 · 248832
Positional
248832 · 20736 · 1728 · 144 · 12 · 1

Side notes...

• Latitude and longitude are heavily reliant on the number 12 and its multiples and composites.
• Dice probability theory loves the number 12 composites.
• Astrology, the zodiac, and ancient cultures recognized the uniqueness of the number 12.

More Duodecimal, Dozenal, Base 12 to Base 10 Conversion Examples

0=0	92=110	B00=1584
1=1	100=144	BBB=1727
5=5	101=145	1000=1728
9=9	110=156	1001=1729
A=10	200=288	1010=1740
B=11	202=290	1100=1872
10=12	20A=298	1111=1885
11=13	20B=299	2000=3456
18=20	210=300	42BB=7343
20=24	7B6=1146	AB2B=18899
5A=70	A00=1440	B460=19656
5B=71	A2B=1475	BBBB=20735

Convenience relist...

Base 12, Duodecimal Orders of Magnitude
1 · 12 · 144 · 1728 · 20736 · 248832
Positional
248832 · 20736 · 1728 · 144 · 12 · 1

The Dozenal Society of America has all sorts of information regarding the mathematical and societal aspects of the base twelve number, counting system.

Some of the Comments from the Previous Hosting Platforms

• Commenter, Will Apse, said: I'm a bit weird about the number 12. As a kid I used pounds, shillings, and pence for money with 12 pennies in the shilling and twenty shillings in the pound (decimalized when I was 12, lol). This might be why I often think about the oddities of 12's. Money and time are rather important.
• Commenter, DreamerMeg, said: I was brought up in the UK pre decimal money, same as Will Apse, but it's still difficult for me to get my head round the idea of base 12.
• Commenter, BradMastersOCcal, said: Binary to base 12 is not as clean as base 8 (3 bits) or 16 (4 bits); this allows binary to just overflow into the next number. Base 12 has to use 4 bits but stop at 1011 (B). It is more like BCD. I had no idea this was a popular common base. Thanks, it is a very interesting article.
• Commenter, DreamerMeg , said: As a child, we had to learn to count in 12's for the UK's monetary system. Counting in 10's is a lot easier. We had a class of 7-year-olds chanting 12 pence is 1 shilling, 18 pence is 1 and sixpence, 24 pence are two shillings, 30 pence is 2 and sixpence, 36 pence is three shillings! The UK went decimal in 1971 but I can still calculate between new money and old money and between decimal measurement systems (SI units) and the old pounds and ounces. Keeps the brain active, but I don't know that it's useful. Good article.

Side Note. Selecting the relevant Label Menu option below provides a much-expanded list of resources. You can then select one of the listed page titles to make it standalone.

- End of Article -

Re: Using Mobile?
Home: site intro and featured articles/resources.
View Web Version: displays Main Menu article categories (will be located below), additional site info (below and side), search function, translation function.

I first published this article at another website on 11/17/2013. However, to keep the information current, relocating to websitewithnoname.com was best. This copyrighted tutorial has served people well for years.

MPH to FPS: Mental Math Calculation Conversion Formula for Miles per Hour to Feet per Second

Latest update: November 28, 2024. Page URL indicates original publication date; meanwhile, times change, and the updates continue.

How to Instantly Convert MPH to FPS While Driving

- The Quick and Easy Math Trick Formula Equation -

Simply divide miles-per-hour by 2, then multiply the result by 3 to find feet-per-second.

This is the easy, quick math formula or equation to use and gives a usable, fairly accurate answer. Your answer will be accurate within 5%. As an example, 100 mph converts to 150 fps. If one does the more complicated method of math calculation (detailed further down the page), the resulting answer would be 147 fps.

"How many feet per second..." 
is a math question usually relating to cars and driving.

Easy Table Conversion from MPH to FPS Examples Chart

Divide by 2, then multiply by 3.

MPH	FPS
10	15
15	22.5
20	30
25	37.5
30	45
35	52.5
40	60
45	67.5
50	75
55	82.5
60	90
65	97.5
70	105
75	112.5
80	120
90	135
100	150
120	180
140	210
160	240

The More Difficult (and More Accurate) Answer

To prove the quick math shortcut conversion calculation works:

1. First. convert MPH (miles-per-hour) to MPM (miles-per-minute) by dividing MPH by 60.
2. Then convert miles to feet. There are 5,280 feet in one mile, so multiply MPM by 5,280 to get FPM (feet-per-minute).
3. Lastly, convert FPM to FPS (feet-per-second) by dividing by 60.

Examples of the Longhand Math Converting Miles-per-Hour (MPH) to Feet-per-Second (FPS)

MPH to FPS Math Conversion Example One

You're going 25 mph. How many feet is that per second?

1. Conversion from mph to fps is as follows: If we divide by 60, we get miles-per-minute (mpm): 25/60 = .416667.
2. For accuracy's sake, now is a good time to convert miles to feet. There are 5,280 feet in a mile so we multiply mpm times 5,280 to get feet-per-minute: 416667 x 5280 = ~2199.99 feet-per-minute [note: "~" means approximate].
3. To convert from feet-per-minute to feet-per-second (fps), we divide the answer by 60: 2199.99/60 = ~36.667 feet-per second.
4. This answer is within 5% of the one you get doing the mental easy math way, which says 25 mph divided by 2 and then multiplied by 3 equals 37.5 fps.

MPH to FPS Math Conversion Example Two

65 mph. How many feet per second?

1. Conversion from mph to fps is as follows: If we divide by 60, we get miles-per-minute: 65/60 = 1. 0843333333333.This makes sense. After all, 60 miles an hour is the well-known mile-a-minute.
2. For accuracy's sake, now is a good time to convert miles to feet. There are 5,280 feet in a mile, so we multiply the miles-per-minute times 5,280 to get feet-per-minute: 1.0843333333333 x 5280 = ~5725.28 feet-per-minute.
3. To convert from feet-per-minute to feet-per-second, we divide the answer by 60: 5725.28/60 = ~95.421 feet-per second, which is the answer.
4. This coincides within 5% of the table above, which says 65 mph equals 97.5 fps. 

MPH to FPS Math Conversion Example Three

120 mph is how many feet per second? Conversion from mph to fps is as follows.

1. If we divide by 60, we get miles-per-minute: 120/60 = 2.000. This again makes sense; 60 miles an hour is the usual mile-a-minute. So 120 mph would be 2-miles-a-minute.
2. To convert miles to feet. There are 5,280 feet in a mile, so we multiply the miles-per-minute times 5,280 to get feet-per-minute: 2 x 5280 = ~10560 feet-per-minute.
3. To convert from feet-per-minute to feet-per-second, we divide the answer by 60: 10560/60 = ~176 feet-per second.
4. This number is within 5% of the table above which says 120 mph equals 180 fps.

The Reverse FPS to MPH Math Conversion Examples

Quick way to find reverse, i.e., convert from feet-per-second to miles-per hour: divide fps by 3 and then multiply by 2 for mph.

Easy Table Conversion from FPS to MPH Examples Chart

FPS	MPH
10	6.67
20	13.33
25	16.67
40	26.68
50	33.33
75	50
100	66.67
150	100
200	133.33
500	333.33
1000	666.67

Doing 20 miles-per-hour? That is 30 feet-per-second.

The laws of physics seldom take a vacation.
Most of these cars would not be able to stop in time.

- End of Article -

Re: Using Mobile?
Home: site intro and featured articles/resources.
View Web Version: displays Main Menu article categories (will be located below), additional site info (below and side), search function, translation function.

How Much Does a Pint / Quart / Gallon Weigh in Pounds?

Latest update: November 30, 2024. Page URL indicates original publication date; meanwhile, times change, and the updates continue.

How Many and How to Calculate Pints, Quarts, Gallons to and from Pounds

Alternate Titles or Questions

• How to Convert Pints to Quarts to Gallons to and from Pounds?
• Volume to Weight Conversions or Weight to Volume Conversions – 8:4:1:8.
• How many pounds in X pints, quarts, or gallons?
• How much does X gallons, quarts, or pints weigh?

A list of most-searched-for questions and answers is included. There is also a specific section relating to the calculating of the size/volume/weight of home water heaters.

Volume to Weight Conversions. Weight to Volume Conversions.
Simple math to convert or calculate pints, quarts, gallons, and pounds.

Be advised that this page is US-centric. As an example, this does not work in the UK where a pint is 1.25 pounds as opposed to US 1.043 pounds at room temperature (RT). There are also issues of temperature and density, both of which are addressed further down the page. The purpose of this page is for practical, everyday business-of-living uses only. For that it will serve you well.

First – The Quick Answers to Volume Amounts and Ratios

Volume Definitions

• 2 pints equals 1 quart.
• 4 quarts equals 1 gallon.
• 8 pints equals 1 gallon.

Or to Put It Another Way...

• 1 quart equals 2 pints.
• 1 gallon equals 8 pints.
• 1 gallon equals 4 quarts.

Converting Volume to Weight

Converting volume to weight has everything to do with the density of the liquid. Fortunately, this question usually has to do with:

• How much does the gasoline in your gas tank or a gas can weigh?
• How much does a specific container of water or other mostly-water grocery items weigh?
• Questions relating to home water heater size, calculated water volume and the resulting weight.

The rule of thumb, and the expression to remember is: "A pint's a pound the world around." The resulting estimates and extrapolations from this rule will serve you well for most everyday purposes. For scientific and industrial purposes where greater accuracy is required, a pint weighs a little bit more than a pound (1.043 lb.).

Basic Formulas

• A pint weighs a pound.
• There are two pints in a quart, so a quart weighs 2 pounds.
• There are four quarts in a gallon, so a gallon weighs 8 pounds. 
• And the eight pints in a gallon, also weighing 8 pounds.

This pretty much answers the question. Here are some other typical examples:

Some Household Examples

• A 1-quart bottle of Gatorade weighs 2 pounds. Note: there are 2 pints in a quart and 4 quarts in a gallon. As a side note: there are 16 fluid ounces in a pint, 32 fluid ounces in a quart; 1 and 2 pounds respectively.
• A 2-liter bottle of Pepsi would convert to a weight of a little over 4 pounds. Note: A liter is slightly more volume than a quart.

Some gallon examples

• A 1-gallon container would convert to a weight of 8 pounds.
• A 5-gallon container weighs 40 pounds.
• A 10-gallon container weighs 80 pounds.
• A full, 25-gallon SUV gas tank means you are hauling around 200 pounds of fuel.
• A typical city water tower can hold anywhere from 300,00 to 600,000 gallons of water, which converts to a weight of 2,400,000 to 4,800,000 pounds of water sitting on those "stilts".

The Density of the Liquid Significantly Affects the Rules Concerning Volume Conversion Calculations to Weight

A major component of converting fluid volume to a weight measurement is the density of the fluid. For gasoline, water, and most grocery items; the rule of a-pint's-a-pound will serve you just fine. However, as an example, the rule probably wouldn't work too well with any significant volume of engine oil. As an extreme example, the liquid metal/element mercury would totally throw the pint's-a-pound rule out the window. So of course would any molten metal or alloy.

Fluid density is also affected by temperature. This is why many people fill their gas tank first thing in the morning. There is more gas per gallon at 50 degrees Fahrenheit than at 90 degrees Fahrenheit. It should be noted the percentage difference is in the low single-digits.

Here is a worthwhile page from NASA about Density, Mass (weight), Volume for both solids and liquids.

List of Frequent Volume-to-Weight Conversion Q&A

The Most-Searched-for Questions and Answers for How Many Pounds

• How much does 1.5 quarts weigh? Answer is 3 pounds.
• How much does 2 quarts weigh? Answer is 4 pounds.
• How much does 3 quarts weigh? Answer is 6 pounds.
• How much does 5 quarts weigh? Answer is 10 pounds.
• How much does 6 quarts weigh? Answer is 12 pounds.
• How much does 10 quarts weigh? Answer is 20 pounds.
• How much does 16 quarts weigh? Answer is 32 pounds.
• How much does 5 gallons weigh? Answer is 40 pounds.
• How much does 10 gallons weigh? Answer is 80 pounds.
• How much does 15 gallons weigh? Answer is 120 pounds.
• How much does 20 gallons weigh? Answer is 160 pounds.
• How much does 50 gallons weigh? Answer is 400 pounds.
• How much does 55 gallons weigh? Answer is 440 pounds.

• How many pints is a pound? Answer is 1.0 pint.
• How many quarts is a pound? Answer is 0.5 quarts.
• How many gallons is a pound? Answer is 0.125 gallons.

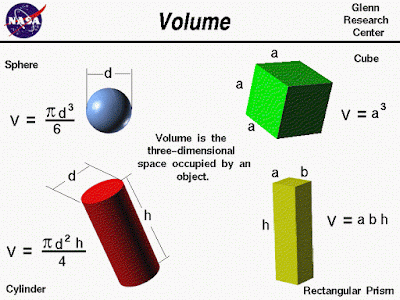The formulas for the volume of a sphere, the volume of a cube,
the volume of a cylinder, the volume of a rectangular prism.

More Water and Gasoline Volume-to-Weight Examples

Depending on what unit of measurement you use, volume will equal cubic English or cubic Metric; examples being cubic inches or cubic centimeters.

Side note: the tilde (~) is the mathematical symbol for approximate.

English

• 29 cubic inches equals ~1 pint, which equals ~1 pound.
• 58 cubic inches equals ~2 pints, which equals ~1 quart, which equals ~1/4 of a gallon, which equals ~2 pounds.
• 231 cubic inches equals ~4 quarts, which equals 1 gallon, which equals 8 pounds.

Metric

Most of the world uses metric. There is a reason for that. As an example, 1000 cubic centimeters equals one liter, 1000 grams equals one kilogram, etc.; all nice, neat, and tidy. The United States and others are trying to get with the program; metric is already included with English measurement on most U.S. consumer items.

How Much Does the Water Weigh in a Full Water Heater?
– Water Tank Size Volume Formula and Answers –

Serendipitous energy.gov page on everything about water heaters, including how to buy one.

How to Calculate the Weight of the Water in a Home Water Heater

How much does the total amount of water in a water heater weigh, volume to weight conversion.

From the above NASA chart we see the volume formula for a cylinder is V = (πd2h)/4.

Water tank heaters come in all sizes. For the purposes of this example, we will say the water tank heater has a measured height of approximately 54 inches; what with this, that, and the other, the water part is probably around 48". The diameter measured as 18"; what with insulation, etc., 16 probably works.

So,
d = 16
h = 48

Thus (" * " meaning to multiply),
V = (3.14 * 16 * 16 * 48) divided by 4.

Since all numbers are inches, the answer will be in cubic inches. We reduce the formula as follows:

1. V = (3.14 * 256 * 48) divided by 4.
2. V = (3.14 * 12288)/4
3. V = 38514/4
4. V = 9646 cubic inches

231 cubic inches is equal to a gallon, so we divide 9646 by 231.
9646/231 = 41.76 gallons.

What with the inner measurements being estimates, looks like it is a 40 gallon water heater.

1. A gallon weighs 8 pounds.
2. So multiplying 40 times 8 gives 320.
3. A 40-gallon water heater contains 320 pounds of cold water.

Knowing the volume and weight of a 40-gallon water tank heater makes it easy to extrapolate the volume and approximate weight of other water heaters. Do remember that as volume increases, the discrepancy totals of the  "pints-a pound". designation versus the more accurate 1.043 lb. designation also increases. As an example: multiplying the 320 lb. calculation for a 40 gallon water heater by 1.043 gives a result of 333.76 lb. at RT versus the original approximation of 320 lb. at RT. When the water temperature is at hot water heater level, the actual weight will fall between the 320 lb. calculation and the 333.76 lb. calculation.

• 10 gallon water heater is 2310 cubic inches and the water weighs 80 pounds.
• 20 gallon water heater is 4620 cubic inches and the water weighs 160 pounds.
• 30 gallon water heater is 6930 cubic inches and the water weighs 240 pounds.
• 40 gallon water heater is 9240 cubic inches and the water weighs 320 pounds.
• 50 gallon water heater is 11550 cubic inches and the water weighs 400 pounds.
• 80 gallon water heater is 18480 cubic inches and the water weighs 640 pounds.
• 100 gallon water heater is 23100 cubic inches and the water weighs 800 pounds.

Do keep in mind the temperature versus density considerations and the expansion of water when heated, i.e., a fully hot water heater tank weighs slightly less than a cold or warm water tank heater that's been freshly refilled after usage. The difference between hot and cold water density versus volume is significant enough that most water heaters have a temperature pressure relief valve and a drainage tube or pipe to compensate for this.

Converting Cubic Inches to Cubic Feet...

...and the corresponding volume and weight ratios. It is surprising how much just one cubic foot of water weighs.

With the pint-equals-pound rule, one cubic foot of water weighs 60 pounds for approximation purposes.

A cubic foot is 12 inches times 12 inches times 12 inches. So 1728 cubic inches equals 1 cubic foot. To convert cubic inches to cubic feet, simply divide the cubic inches by 1728. So using the above examples, we would have:

• 2310 cubic inches equals 1.34 cubic feet equaling 10 gallons equaling 80 lb.
• 4620 cubic inches equals 2.68 cubic feet equaling 20 gallons equaling 160 lb.
• 6930 cubic inches equals 4.02 cubic feet equaling 30 gallons equaling 240 lb.
• 9240 cubic inches equals 5.36 cubic feet equaling 40 gallons equaling 320 lb.
• 11550 cubic inches equals 6.70 cubic feet equaling 50 gallons equaling 400 lb.
• 18480 cubic inches equals 10.72 cubic feet equaling 80 gallons equaling 640 lb.
• 23100 cubic inches equals 13.40 cubic feet equaling 100 gallons equaling 800 lb.

* A side note. I happened to stumble across this on Wikipedia: "Pound (mass), a unit of mass often abbreviated incorrectly as 'lbs' in the plural. Abbreviations of units of measure do not use an 's' on the end for plural."

May all your calculations be prosperous ones.

- End of Article -

Re: Using Mobile?
Home: site intro and featured articles/resources.
View Web Version: displays Main Menu article categories (will be located below), additional site info (below and side), search function, translation function.

How to Remember Color Order of Visible Spectrum and Rainbow - ROYGBIV

Latest update: November 30, 2024. Page URL indicates original publication date; meanwhile, times change, and the updates continue.

Remembering the list order of the rainbow and visible light color spectrum is easy: ROYGBIV.

Additional wavelength, rainbow, sunset, laser images and information resources were added afterwards for folks who might find them interesting. But first, The Quick and Easy Way to Remember Rainbow and Spectrum Colors...

An Introduction to Mr. Roy G. Biv

Mnemonic Trick to Remember the Order of Colors in the Visible Light Spectrum and Rainbows

His name is Roy G. Biv.

Note the first letter of each color in the visible light color spectrum map above. If you can remember the name, Roy G. Biv, then you have accomplished your goal.

ROYGBIV - The Color List and Order of the Visible Light Spectrum and Rainbow

• Red, Orange, Yellow, Green, Blue, Indigo, Violet

If you are interested in more information about the visible spectrum, wavelengths, light, colors, etc.; there are all sorts of additional information and resources below.

The List and Order of Visible Spectrum Wavelengths

Visible light wavelengths

• Red: The lower and longer wavelengths
• Violet: The higher and shorter wavelengths

An Expanded Electromagnetic Spectrum List

There really isn't that much more to it.

• Gamma Rays
• X-Rays
• Infrared
• Red, Orange, Yellow, Green, Blue, Indigo, Violet
• Ultraviolet
• Microwaves 
• Radio Waves

Interesting how the visible spectrum is right in the middle. As a side note, there are two categories of ultraviolet light; long wave and short wave; UV lights can be purchased that radiate both wavelength ranges.

This is a good time to mention that ultraviolet light can permanently damage your eyes. Never stare directly at a UV light. The damage can occur over time. A mistake you make when you are 20 years old can come back to haunt you in your later years, For that matter, most people who wear glasses or contacts always get a UV-blocking coating on their lenses and/or contacts. And for those who use sunglasses, always buy a reputable brand that has the UV protection coating.

Here is a short article dedicated exclusively about ultraviolet light and your eyes: Things That Reflect or Emit Ultraviolet Rays.

An Expanded Electromagnetic Wavelength Image

This image came from a NASA page with all sorts of additional information and resources included, well worth a visit.

Rainbows - Nature's Natural Prisms

This NOAA/NASA page will tell you everything you would ever want to know about rainbows, how they are formed, etc. Rainbow images are free and in the public domain.

Symmetric Rainbow

Double Rainbow

Rainbow over the Gardner River Canyon near Mammoth NPS photo by Neal Herbert

Light Show Sunsets

This NOAA/NWS page explains the causes for the vivid sunsets we sometimes see. Sunset images are free and in the public domain.

Sunset image

Sunset image

Sunset image

Sunset image

Lasers - Otherwise Known as Light Waves With an Attitude

Here is an introductory page on How Lasers Work. Laser images are free and in the public domain.

Ground-to-Space Laser Calibration System

NASA page on ground-based systems to calibrate Earth observing sensors
measuring reflected radiance in low and geostationary orbits.

Simulation of Laser-Plasma Interaction

ALCF page on laser-plasma interactions and current projects.

Lasers Used in Dual Atomic Clock

NIST page on how lasers are used in atomic clocks.

It is hoped you liked the images and additional information resources. Feel free to use these public domain images as desktop or other screen backgrounds, Pinterest pinning, other social media uses, etc.

So, what is the order of colors in a rainbow or the visible light spectrum?

- End of Article -

Re: Using Mobile?
Home: site intro and featured articles/resources.
View Web Version: displays Main Menu article categories (will be located below), additional site info (below and side), search function, translation function.

Selecting the relevant Label menu option provides additional articles.